通常、定常流のシミュレーションは、初期設定の状態(仮定した流れ場)から定常流れ場に達するまで計算を繰り返すことで行っている。これを “iterative convergence (繰り返しの収束)” と呼ぶが、収束したと判断するために基準値を設定することが求められる。
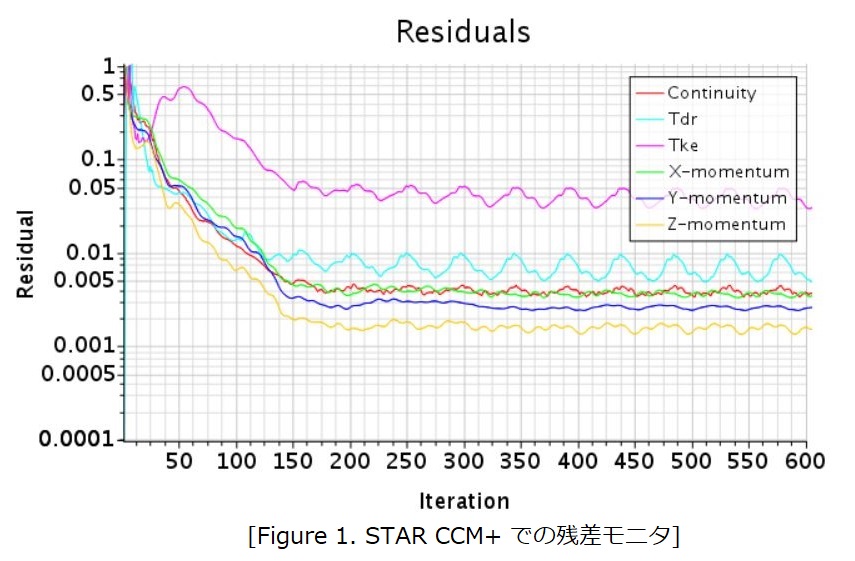
- Residuals / 残差
- Results
- Time accurate simulation
- Space marching simulation
Spatial convergence の評価とは、CFD simulation における離散化誤差のオーダを特定すること、と言える。(なお、spatial convergence study は、grid convergence study、grid refinement study とも言う。)
グリッドの品質が良くなるほど(セルが小さくなって、流れ場のセル数が増えるほど)、空間、時間に対する離散化誤差が小さくなる。
Grid convergenceのオーダは、the discrete solution と the exact solution の差として定義される解の差(solution error)であり、それぞれのグリッド $h$ について (eq.1) で表すことができる。
CFD code は、理論上のconvergence orderを得るための数値計算アルゴリズムを利用している。しかしながら、数値モデル、境界条件、グリッド、それぞれのオーダが影響するために、結果として観測されるconvergence orderは理論値よりも小さくなる。
$C$は定数、$h$はgrid spacing、$p$ は収束の次数を表す。また、上の式について、$p$ は、$ \log(h)$ に対する $ \log(E) $の曲線勾配から求めることができる。ただ、(eq.2) から $p$ を求めるためにはプロットするためのデータが大量に必要だし、グラフのプロット自体の精度の問題も出てくる。そこで、グリッド間隔の比(grid refinement ratio) $ r $ を使って以下の通り $p$ を直接求める。
この精度は、打ち切り誤差と離散化の度合いによって決まる。また、局所的な精度(local order of accuracy)はそれぞれのグリッドについて、離散化を計算した時の精度で決まるが、全体の精度(global order of accuracy)は前処理の結果の影響を受けるので、局所的な誤差よりも小さくなる(通常、1桁小さい)。
ちなみに、grid refinement ratio, $ r $ の値が未知数で、あるグリッドが既知のグリッドよりも小さい/大きい時、effective grid refinement ratio(変化率)は以下の式で表される。
ただし、$ N $ はグリッドポイントの総数、$ D $ は流体ドメインの次元を表す。
今では一般に知られるようになった、Grid Convergence Index (GCI) という概念は、参考文献の Patrick J. Roache によって考案されたもの。これによると; “The basic idea is to approximately relate the results from any grid refinement test to the expected results from a grid doubling using a second-order method. The GCI is based upon a grid refinement error estimator derived from the theory of generalized Richardson Extrapolation. It is recommended for use whether or not Richardson Extrapolation is actually used to improve the accuracy, and in some cases even if the conditions for the theory do not strictly hold.”
GCI とは、コンピュータが算出した値が、漸近値からどのくらい離れているかを表す指標のこと。これによって、グリッドの品質向上によってどれくらい誤差の領域が変わるかを数値で示すことができる。GCI が小さいほど、それが漸近値領域に近いといえる。
細かいグリッドの GCI は次の式で定義される。
式の導出については、Richardson extrapolation (外挿法を使った近似推定の方法で、CAEの計算で使われるので有名)の説明が必要なので、こちらについては別途 → Richardson Extrapolation
$ \epsilon $ はRichardson extrapolation によって算出される相対誤差、$ F_{s} $ はセーフティファクタを表す。(これまでの研究から、2 gridsの時は、$ F_{s} = 3.0 $、それ以上の場合は $ F_{s} = 1.25 $ が好ましいとされている。) $ p $ は上述の通り。
Roache, P.J., Ghia, N. K., and White, F. M. (1986) “Editorial Policy Statement on the Control of Numerical Accuracy”, ASME Journal of Fluids Engineering, Vol.108, No.1., pp.2.