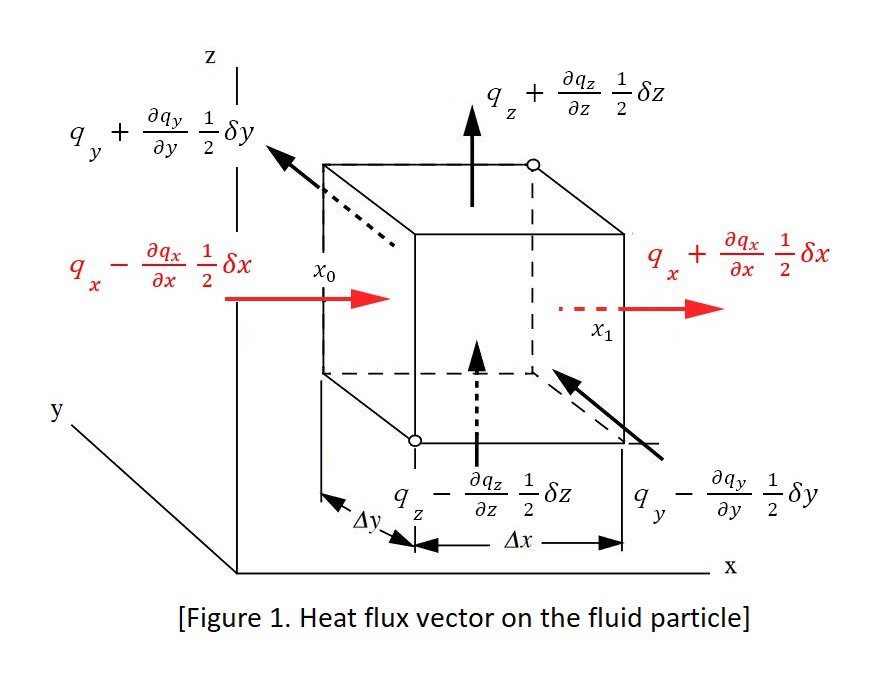
熱伝導によるエネルギーの変化量について考える。熱流束のベクトルを ${\bf q} = (q_{x}, q_{y}, q_{z}) $ とする。まず、$x$ 軸方向について、微小流体の受ける熱の正味伝達率は、Figure 1 の示す通り、面 $x_{0}$ から入ってくる割合と面 $x_{1}$ から出ていく割合の差で表される。
A heat flux vector is defined as ${\bf q} = (q_{x}, q_{y}, q_{z}) $ to consider the energy flux due to heat conduction. Firstly, the net rate of the heat transfer to the fluid particle in the x-axis direction can be expressed as the difference between the rate of heat transferred to the surface $x_{0}$ and the rate of heat radiated from the surface $x_{1}$ .
y, z軸方向についても同様にして、以下の通り求めることができる。
Similarly, the net rates of heat transfer in the y, z directions can be obtained respectively.
単位体積あたりの熱量増加率は、その微小流体の境界を通った熱の合計を体積 $ \delta x \delta y \delta z $ で割ったものなので
The total rate of heat transferred to the fluid particle per an unit volume is the sum of the above divided by the volume $ \delta x \delta y \delta z $
また、フーリエの法則から、熱流束は局所温度 $T$ の勾配を使って表すことができるので、
From the Fourier’s law, the heat flux can be described with the gradient of the local temperature,
(eq. 2), (eq. 3)から、微小流体における熱伝導による熱量の変化率は以下の通り示すことができる。
Finally, the rate of the heat transfer to the fluid particle can be obtained from (eq. 2) and (eq. 3).