主成分分析 (Principal Component Analysis)

Principal Components Analysis (PCA) is widely used statistical techniques for data analysis because it is very useful for the dimensionality reduction, visualization and compression.

主成分分析 (PCA) という統計手法を使うことによって、次元削減や視覚化、データ圧縮が可能になるので、現在、いろんな分野で幅広く使われています。

FYI: In this page, $X_{n} \equiv (X_{n}^1, X_{n}^2, …, X_{n}^d)^T$

I think this expression is normal way when we study multivariate analysis, it can save writing space 🙂

Heuristics / 導出

When we have a sample dataset (experimental data, etc.), $X_{n}$, and $X$ represents a $d$-dimensional vector, a cloud of points in $\mathbb{R}^d$ consists of them. (In terms of practical use, basically $d$ is quite large, so not possible to visualize them.) So, let’s consider how to project the cloud onto a sub-space of dimension $d’$ by keeping as much as details as possible ($ d’ < d$).

対象のデータセット（実験データなど）, $X_{n}$ が$d$次元ベクトルで表される時、$X_{n}$は $\mathbb{R}^d$ に含まれるポイントからなるクラウドを構成する。（実務レベルで見ると、実際、$d$はかなり大きい数であることが多いので、3次元以下の場合のように視覚化することができない。）そこで、できるだけオリジナルデータの詳細を失わないように、次元を$d’$に下げる方法を考えてみる。

Introduce the equation below.

$S = PDP^T$

where $ P = (v_{1}, v_{2}, …v_{d})$ is an orthogonal matrix, and

$ D = \left( \begin{array}{cccc} \lambda_{1} & 0 & \cdots & 0 \\ 0 & \lambda_{2} & 0 & \vdots \\ 0 & \cdots & \ddots & 0 \\ 0 & \cdots & 0 & \lambda_{d} \end{array} \right)$ with $\lambda_{1} \geq … \lambda_{d} \geq 0$

FYI: Practically, $ \lambda_{p} $ is an empirical variance of the $v_{p}^T \textbf{X}_{i}’s$, with $p = 1, 2, …$ etc.

Thus, each $\lambda_{d}$ represents the spread of the cloud in the $v_{d}$ direction. $v_{1}$ maximizes the experimental covariance of $\textbf{a}^t \textbf{X}_{1}, \textbf{a}^t \textbf{X}_{2} …, \textbf{a}^t \textbf{X}_{n}$ over $\textbf{a} \in \mathbb{R}^d$.

Summary of Procedures / 手順の概要

Input $\textbf{X}_{1}, \textbf{X}_{2}, …, \textbf{X}_{n}$
$n$ points in $d$ dimensional space.
Calculate dataset of samples (experimental data, etc.) as a converiance matrix.
対象となるデータ（実験データなど）を共分散行列として演算。
Calculate the decomposition $S = PDP^\mathrm{T}$
where $D = Dig(\lambda_{1}, \lambda_{2}, …, \lambda_{d})$ and $P = (v_{1}, v_{2}, …, v_{d})$ is an orthogonal matrix. Also $\lambda_{1} > \lambda_{2} > … \lambda_{d}$
Choose $k$ and define $P_{k} = {v_{1}, v_{2}, …, v_{k}}$
where $ k < d $ and $ P_{k} \in \mathbb{R}^{d \times k} $
Obtain $\textbf{Y}_{1}, \textbf{Y}_{2}, …, \textbf{Y}_{n}$
where $\textbf{Y}_{i} = P_{k}^\mathrm{T} \textbf{X}_{i} \in \mathbb{R}^k$

First Principal Component / 第１主成分

$ \textbf{v}_{1} \in$ argmax $\textbf{u}^\mathrm{T} S \textbf{u}$ where $\|\textbf{u}\| = 1$

$ \textbf{v}_{2} \in$ argmax $\textbf{u}^\mathrm{T} S \textbf{u}$ where $\|\textbf{u}\| = 1, \textbf{u} \perp \textbf{v}_{1}$

Therefore

$ \textbf{v}_{d} \in$ argmax $\textbf{u}^\mathrm{T} S \textbf{u}$
　　　where $ \|\textbf{u}\| = 1, \textbf{u} \perp \textbf{v}_{j}, j = 1, 2, …, d-1$

NOTE: The $k$ orthogonal direction is the most spread out correspond to the eigenvectors which can be obtained with $k$ largest values of $S$.

FYI: The difference from the least squares method is shown in Figure 1.

[Figure 1. Comparison between LSM and 1st principal component of PCA]

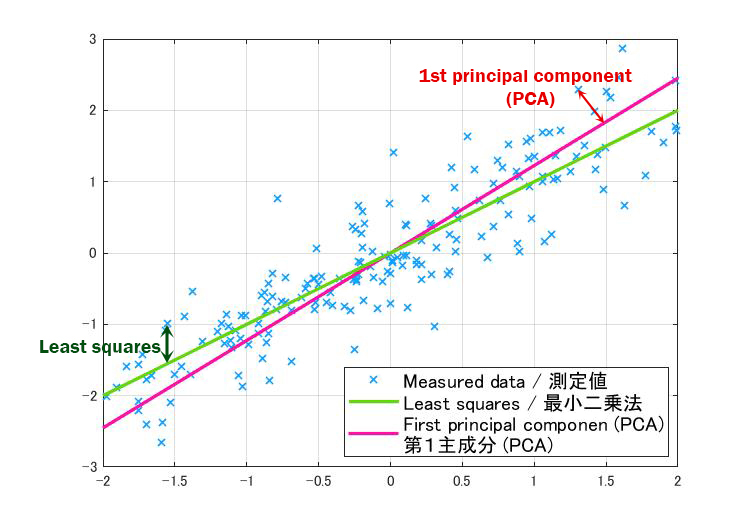
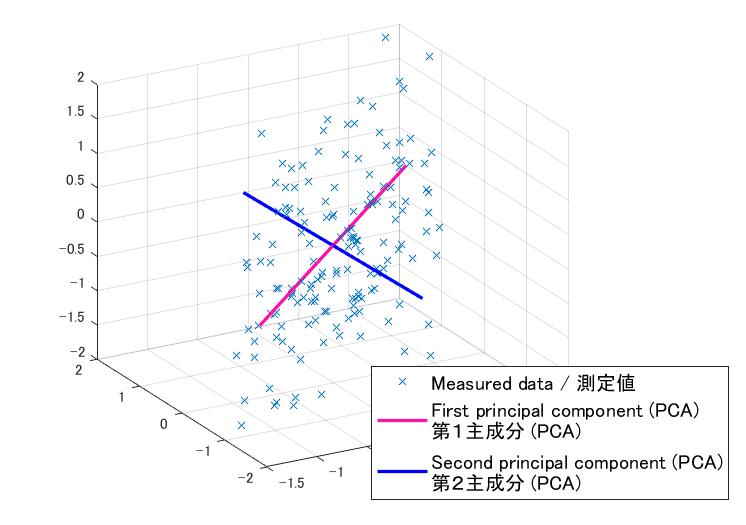
The variance is shown as a red arrow in Figure 1. Find a line (illustrated in pink) to minimize it.

Example of Dimension Reduction (3D to 2D)

Similarly, find a second principal component. Get a transverse line (plotted in blue) by minimizing the variance. From these 2 lines (in other words, 2 equations), a plate can be obtained.