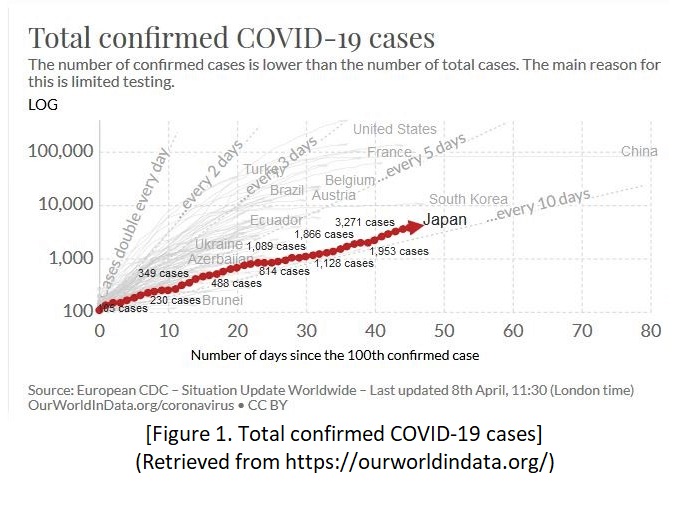
Modelling – Example with COVID-19 Data

modelling の（手順の）概念を実感するために、今回はCOVID-19 の報告データを使って考えてみよう。今回は初心者向けなので、ファクタについては考慮しません。Figure 1 は感染者数の推移を国別にプロットしたデータ（Our World in Data, 2020）。こうやって他国と一緒に表示すると、日本の感染者数は一見、線形モデルで表せるように見えてしまう…

Hope this is helping to understand how to proceed modelling :)　- But this is for beginners, so external factors are not considered in this case.

covid-19-reportdata

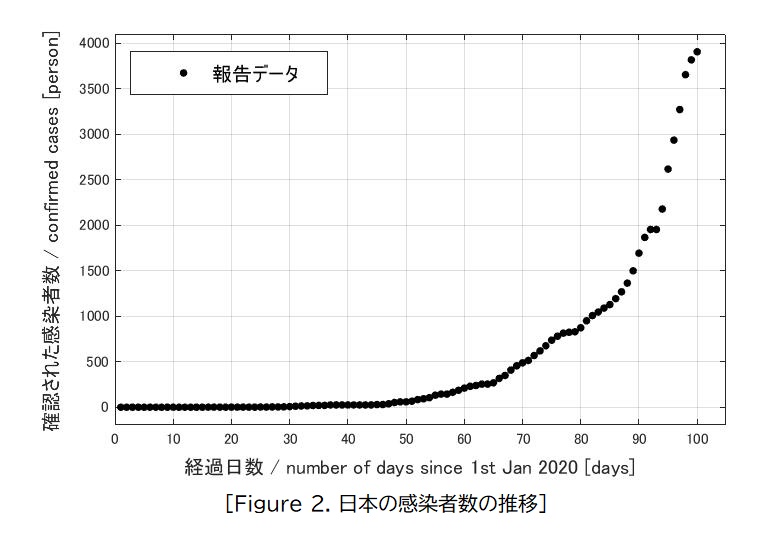
けど、日本のデータだけに絞ってプロットすると、線形モデルでの近似は相応しくないことは一目瞭然。（ちなみに、データはOur World Dataのサイトからcsvでダウンロードしたもの。）なんとなく、指数関数で表せそう？だけど、適当に近似するのもよくないので、累積感染者数は経過日数の関数として表されると仮定してモデル化してみる。

Japanese confirmed CODIV-19 cases against the elapsed time (in days) are illustrated in Figure 2. It seems that the number of cases can be described as an exponential function model, but approximation should be implemented theoretically. Therefore, firstly, it is assumed that the cumulative number of cases can be expressed as a function of the elapsed time to obtain a function for the modelling.

reported_data_Japan_only

累積感染者数は経過日数 $t$ の関数として表すと仮定したので

The cumulative number of reported cases was assumed as a function of the elapsed days, $t$.

$ N(t) = \sum_{s=0}^{t} M(s) $　　　　　　　　　　　　　・・・(eq. 1)

すると、その日の感染者数は

The number of daily reported cases is

$N(t) – N(t-1)$

ここで、その日の感染者（累計ではなく、その日新たに報告された数）は、その日の累計者数の定数 $c$ 倍で表せると仮定する。

Assumed the number of reported cases per day (* not cumulative population) is proportional to the current cumulative cases.

$ N(t+1) – N(t) = cN(t) $
$ N(t+\Delta t) – N(t) = c \Delta t N(t) $
$ \frac{N(t+\Delta t) – N(t)}{\Delta t} = c N(t) $　　　　　　　　　　　　・・・(eq. 2)

(eq. 2) can be described by the ODE.

$ \frac{dN(t)}{dt} = cN(t) $
$ \frac{1}{N(t)} \frac{dN(t)}{dt} = \frac{d\log(N(t))}{dt} = c $
$ \int d \log(N(t)) – \log(N(t_{0})) = c(t – t_{0}) $
$ N(t) = N(t_{0} c^{c(t – t_{0})})$

From the above, the number of daily reported cases is obtained by the ODE, and (eq. 3) means the model is expressed as an exponential function.

$ M_{t} = a e^{ct}$　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・(eq. 3)
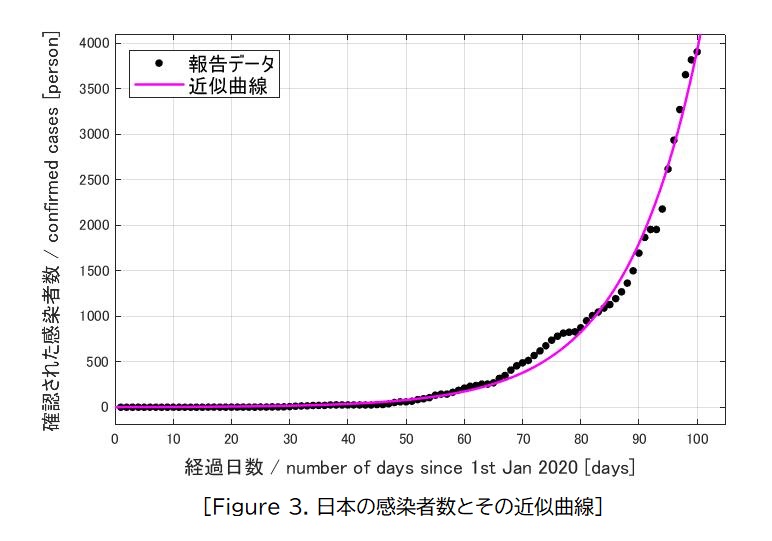
Japanese_covid19_reported_model

(eq. 3) から、このモデルは指数関数として表すことが適切だと確認できたので、MATLABを使って、指数関数で近似した結果が Figure 3。近似の結果、定数はそれぞれ、$a = 1.61, c= 0.078$。

Figure 3 illustrates the model of the number of cumulative cases. It was obtained by the exponential approximation on MATLAB. Consequently, the model is

$ M_{t} = 1.61 e^{0.078 t}$