線形回帰 (Linear Regression Model)

変数 $x$ が統計的に、$Y$ と因果関係のある変数 (the response variavle) であり、線形の関係を持つとき、そのモデルは次の式で表される。

$Y _{i} = β _{0} + β _{1} x _{i} + ε _{i}$ 　　　　(eq. 1)

ただし、

$i = 1, 2, …, n$

(eq. 1) は2つのパーツに分けて考えることができる。 (これが、小学校の教科書にある、 $y=ax+b$ における、 $b$ の部分が $β _{0} $ と $ε _{i} $ に分けられている理由。) まず、 $ β _{0} + β _{1} x _{i} $ について。$β _{0} , β _{1} $ は、それぞれ、線形モデルの切片 (the intercept) と傾き (the slope) を表す係数であり、つまり、 $ β _{0} + β _{1} x _{i} $ はランダムではない。
一方、変数 $ ε _{1}, ε _{2}, ε _{3} $ ,… はランダムで、 $ β _{0} + β _{1} x _{i} $ で表される線形モデルの、それぞれの点の誤差 (errors) として考えることができる。これらの誤差は互いに独立していて、 $ε$ の平均 (mean) は0、分散 (variance) は $ σ^2$ と仮定する。

$ E(ε _{i}) = 0 $ 　　and 　 $ var(ε _{i}) = σ^2 $

以上から、 $ Y_{i} $ もランダムな値をとることになり、

$ E(Y _{i}) = E(β _{0} + β _{1} x _{i} + ε _{i}) = β _{0} + β _{1} x _{i} = μ _{1} $ 　　　　　(eq. 2)

分散 (variance) は次式で表すことができる。

$ var(Y_{i}) = var(β _{0} + β _{1} x _{i} + ε _{i}) = var(ε _{i}) = σ^2 $　　　　　　(eq. 3)

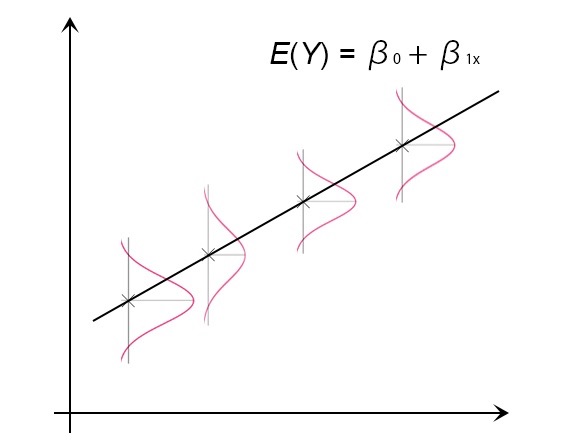
$ E(Y) = β _{0} + β _{1} x $ は “regression function” と呼ばれていて、イメージとしては、以下のようなグラフになる。

車両重量と燃費の関係を考えてみる

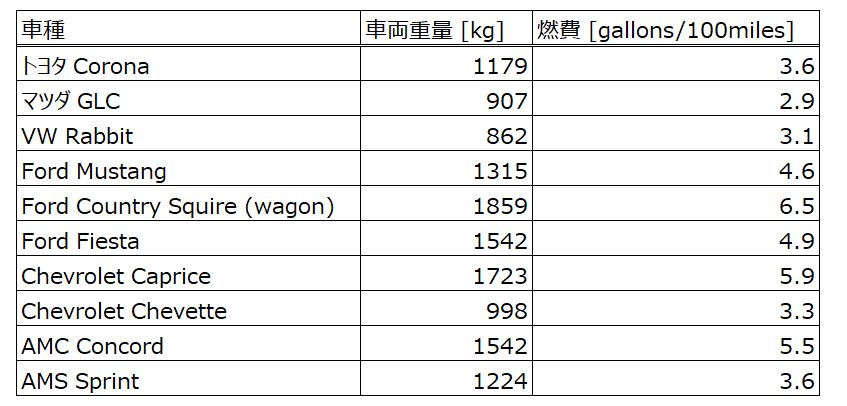
最近の車は特にECUやエンジン内の熱流体技術が向上して、線形データを作りやすい車たちを探すのが大変だったので…ちょっと古い車を対象に検証してみよう。下の表の10車種を対象に考えてみる。（表のデータは1983年 NHTSAのレポートから引用）
車両重量(kg) を $x$ 、燃費(gallons/100miles) を $y$ 、計測数を $n=10$ とする。

list-of-fuel-consumption — [Table 1. 車両重量と燃費]

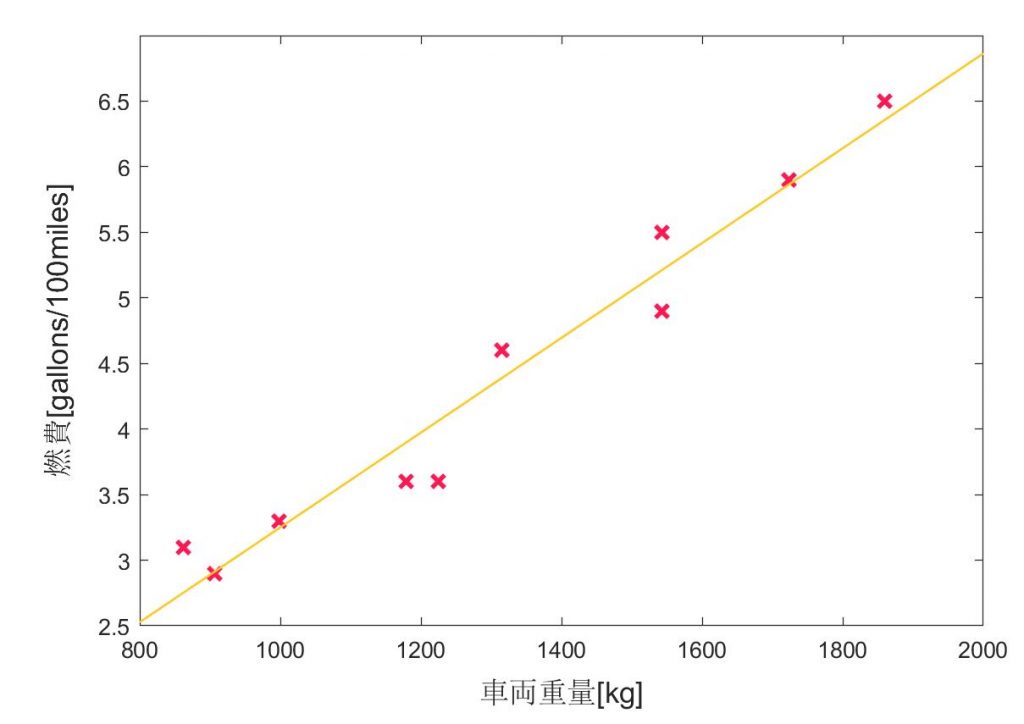
$ y_{i} – β_{0} + β_{1} x_{i} $ の2乗の和は残差線 (Regression line) と測定点がどれほど近いかを表し、この値が最小になるように近似線（オレンジの直線）を決める、というもの。（つまり、全ての測定値（ピンクの $x$ でplotしている点）が線上にある場合、 $ S(β_{0}, β_{1}) $ は0になる。）
また、残差の2乗の和が最小値をとるとき、これを最小二乗推定量 (the least-squares estimates) と呼び、今回の場合は以下のように表す。

$ \hat{β_{0}} , \hat{β_{1}} $

approximated — [Figure 2. 最小二乗法による近似モデル]

$S(β_{0} , β_{1})$ の最小値を知るために、一時導関数 (first partial derivative) を求める。

$ \frac{ \partial S (β_{0} , β_{1}) }{ \partial β_{0} } = 2 \sum_{i = 1}^{n} [ y_{i} – (β_{0} + β_{1} x_{i} ) ] (-1) = 0 $

$ \frac{ \partial S (β_{0} , β_{1}) }{ \partial β_{1} } = 2 \sum_{i = 1}^{n} [ y_{i} – (β_{0} + β_{1} x_{i} ) ] (-x_{i}) = 0 $

上の式を最小二乗推定量の観点から変形すると、

$ \hat{β _{0}} n + \hat{β _{1}} \sum x_{i} = \sum y_{i} $

$ \hat{β _{0}} \sum x_{i} + \hat{β _{1}} \sum x_{i} ^2 = \sum x_{i} y_{i} $

つまり、それぞれの最小二乗推定量は以下の通り定義できる。

$ \hat{β _{1}} = \frac{ \sum x_{i} y_{i} – \frac{ (\sum x_{i})(\sum y_{i}) }{n} }{ \sum x_{i}^2 – \frac{ (\sum x_{i})^2 }{n} } $

$ \hat{β _{0}} = \bar{ y } – \hat{β _{1}} \bar{ x } $

以上から、車両データを計算すると、

$ \sum x_{i} = 13151, 　　　　\sum x_{i}^2 = 18359277, $
$ \sum y_{i} = 43.9, 　　　　\sum y_{i}^2 = 207.31, $
$ \sum x_{i} y_{i} = 61582 $

ただし、n=1 から 10

$ \hat{β _{1}} = 0.003616 $

$ \hat{β _{0}} = 4.39 – \hat{β _{1}} * 1315.1 = -0.3653 $

ちなみに、オレンジ色の近似直線はMATLABのfitting toolを使って簡単にplotできる。