実験データを取り扱ううえで、ランダムな誤差によるscatter(日本語だと散布?)が観測されるのは通常のとこだけれど、中には計測データにトレンドを見いだせないような場合もある。(大学の授業でやるような実験は、既知の法則などを確認するものが大半だから、こういうケースは稀かもしれないけれど。本来の研究では、データがそのファクタと関係あるものなのか?あるのであれば、どんな相関があるのかは自分で考えることになる。)
例えば、左下のグラフは、ぱっと見で $y$ は $x$ の関数として表せる(つまり相関がある)とこが推測できるけれど、右下のような測定結果になれば、きっと、$x$ と $y$ の間には関係がないと考えるだろう。
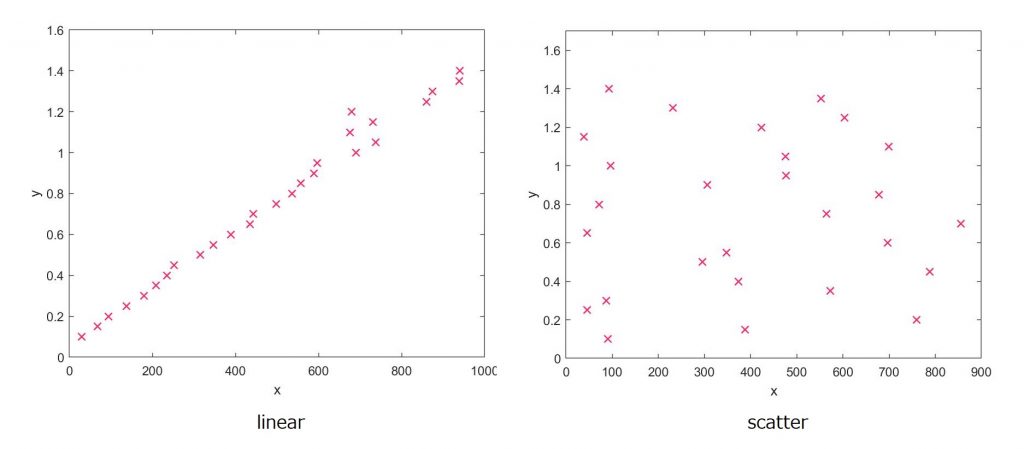
ただ、なんとなくで判断するのはよくない。そこで、統計学では、相関係数(the correlation coefficient), $ r_{xy} $ というものを使って、そこにトレンドがあるという関係の強さを計ることがしばしばある(ここでは、変数 $ x, y $ 間)。変数 $ x, y $ が測定対象の実験について、データセットが $ [(x_{i}, y_{i}), i = 1, n] $ のとき、相関係数は以下の通り定義される。
ただし、
実験データの $ \bar{x}, \bar{y} $ (mean values)を使って相関係数、 $ r_{xy} $ が表されることが分かる。なお、 $ r_{xy} $ は、-1から+1の間の値をとる。(誤差が全く無いなんて現実世界じゃありえないけれど、 $ r_{xy} = +1 $ の場合は完全な線形の関係になる。)
富士スピードウェイを走った時のタイムについて、路面温度と関係があるのかを考えてみる。(人間の運転だから精神状態や体調もラップタイムに影響するけれど、ここでは、まぁ、演習というか遊びなので…)ちなみに、ファクタが増えると、どのファクタの影響で結果(この場合ラップタイム)が変わるかが分からなくなるので、タイヤも含めて車両のセッティングは同じものとする。路面も温度だけが違って、コンディションは全部ドライ。走行データは以下のテーブル通り。

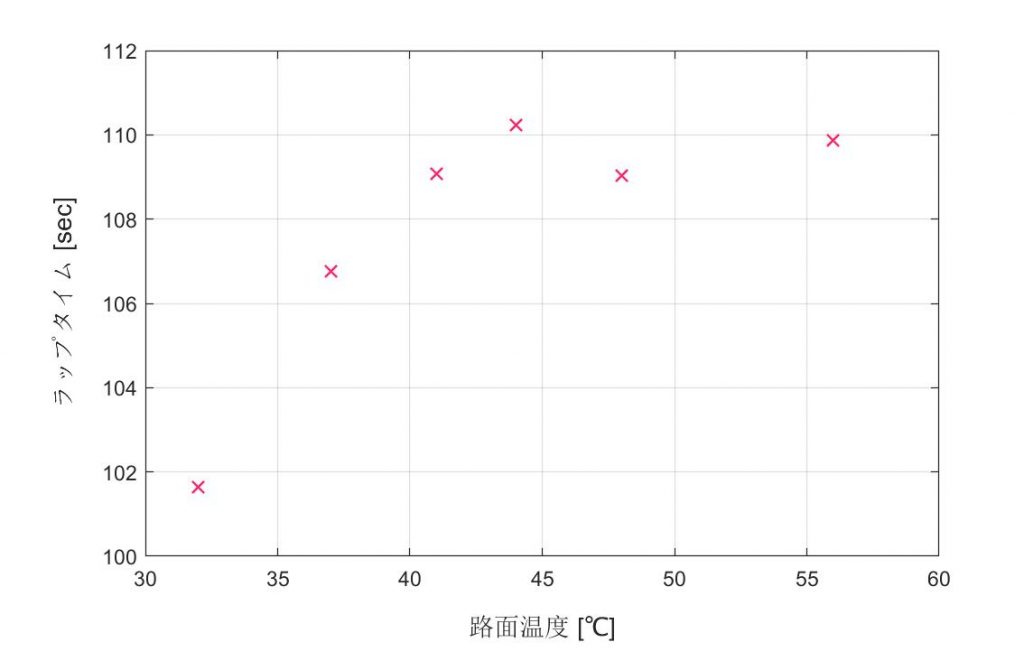
グラフにプロットしてみたものの、見た感じでは、相関関係は一見、弱そう?(そもそもサンプリング数が少ないけれど。)けど、ここは上述の式に則って相関係数(the correlation coefficient)を計算してみる。
というわけで、(たった6回の計測というのが信頼性に欠けるけれど)この走行データを見る限りでは、正の相関が確認できる。