通常、Magic formula というと、タイヤに生じる力を (eq.1) で表すもの、と書いてある。( (eq.1) は補正項を含んでいない最もベーシックな形。)
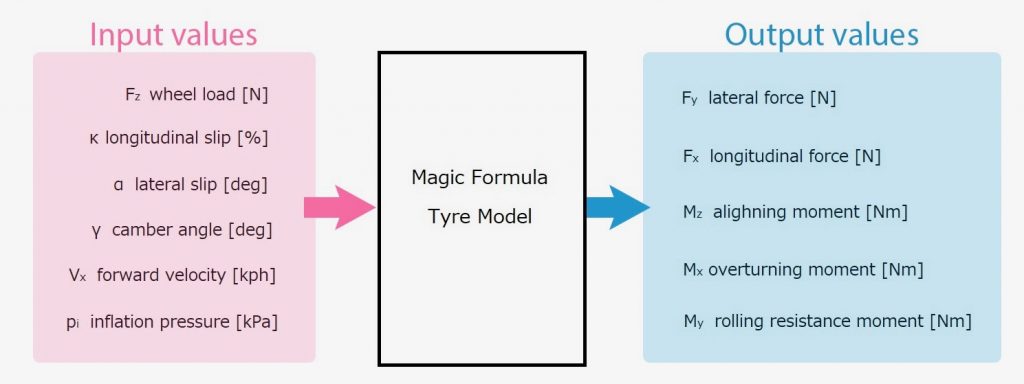
もちろん、この説明は正しい(というか、定義そのもの)。けれど、実際に利用する立場からみると、下の図のイメージが分かりやすいと思う。荷重やスリップ量といった、運転状況(外部環境、ドライバによるコントロール)による値をモデルに入力値としてインプットすると、生じる力(縦力、横力)とモーメントが算出できる、といのが Magic formula というモデル。
$ B, C, D, E $ の Magic formula 係数(オリジナルの表現、coefficientsに従って係数と呼ぶ。また、後述の最適化するためのパラメタ と区別するために、ここではパラメタとは呼ばない。)はタイヤの種類によって異なる。そのため、あるタイヤのシミュレーションモデルを構築する場合、実験データを基に、これらのパラメタを同定する必要がある。(たしか、トヨタがマジックフォーミュラのパラメタ同定装置に関して特許を出していたような…。)
といっても、eq.1 は初期の表現であり、シミュレーション精度を向上させるために多くの研究がなされ、近年、ソフトウェア等で使われているMagic Formulaは、それぞれのMagic formula 係数を更に別のファクタで定義していることが多い。
例えば、pure slip時の縦力について; peak valueを表すMF係数 $ D $ は以下の通り定義することができる。
ここで、 $ F_{z} $ はそのホイールにかかっている負荷[N](インプット値)、 $ \mu_{x} $ は摩擦係数を表す。初期のモデルでは、この摩擦係数は固有値(運転の状況によらず一定)だったけれど、$ \mu_{x} $ は、さらに以下の通り書き表すことができる。
MF係数をタイヤの固有値としてモデリングするのではなく、 $ p_{ Dx1 }, p_{ Dx2 }, p_{ Dx3 }… $ などのパラメタと運転状況によって変わる荷重変化量 $ df_{ z } $ で表現することによって、シミュレーションの精度を向上させている。
なお、ここで、 $ p_{ Dx1 } $ はthe nominal load(基準となる静止状態での論理上の荷重[N])、かつ、キャンバー角 0°、基準内圧状態での縦方向の摩擦係数 。 $ \lambda_{ \mu x } $ は縦力に関する最大摩擦係数のスケールファクタを表す。
これらのパラメタは専用の測定器を使うことで測定し、.tir ファイル(the tyre property file 。テキストとして見ることも可能。)として取得することが可能。しかしながら、”実験データ”は誤差を含むし、専用の装置がない場合も多いので、通常は.tir fileのパラメタをモデリングに直接使うのではなく、生じる力やその時の荷重、角度など、膨大な測定データからパラメタの最適化を行う必要がある(これらのデータは一般的に普及している tyre test rig で取得可能)。
Pacejka, H. B. (2012) Tire and Vehicle Dynamics, 3rd edn., Oxford: Elsevier